Notion de variant et d’invariant de boucle

Document élève

Objectif

L’objectif de cette activité est faire découvrir la notion de correction d’un programme, l’identification des variants et invariants de boucle et de la notion de complexité au travers d’un algorithme simple.

Prérequis

  • Utilisation de l’environnement de développement

  • Type élémentaire : les entiers

  • Structure algorithmique de base : boucle while

Conditions

  • Activité semi-débranchée

  • Niveau première

  • Type d’activité TD/TP

  • Durée : 3h

Rubriques du programme :

  • Algorithmique :

    • Variant et invariant de boucle

    • Cout unitaire et linéaire

  • Langage et programmation :

    • Constructions élémentaires

    • Spécification

    • Mise au point

Introduction

Un programme peut être amené à manipuler un grand nombre de données dont les valeurs peuvent évoluer au cours de son exécution. Il est important de s’assurer que le programme réalise bien le traitement voulu et qu’il s’arrêtera en retournant le bon résultat. C’est par la correction du programme que l’on pourra s’en assurer. Cette correction consiste à trouver :

  • un variant de boucle : condition de sortie d’une boucle

  • un invariant de boucle : propriété logique qui reste vraie de l’entrée de la boucle jusqu’à sa sortie

Variant de boucle

Le variant de boucle est la variable qui croit ou décroit à chaque itération de la boucle. Cette variable comparée à une valeur constante doit permettre de mettre fin à la boucle après un nombre fini d’itérations.

for i in range(10):
    # faire quelque chose

i va croitre de 0 à 9 et la boucle prend fin après la 10ème itération.

    i = 0
    while i < 10:
        # faire quelque chose

Invariant de boucle

L’invariant de boucle est une propriété qui est vérifiée tout au long de l’exécution d’une boucle. Prenons l’exemple de la fonction ci-dessous qui retourne le quotient de la division entière de deux nombres entiers positifs et non nuls :

    def division_entiere(a : int, b : int) -> int:
    ```retourne quotient tel que a = b*quotient + reste```
        if not (a>0 && b>0):
            return None
        reste = a
        quotient = 0
        while reste >= b:
            reste = reste - b
            quotient = quotient + 1
        return quotient

  • Etat des variables en entrée de boucle :

    • a et b sont des entiers positifs non nuls

    • \$reste = a\$ et \$quotient = 0\$

  • Definir un invariant de boucle :

    • \$a = b*quotient + reste\$ devrait toujours être vérifié, ce serait donc notre invariant de boucle.

  • Avant d’entrer dans la boucle : \$a = b*quotient + reste\$ donne :

    • \$a = b*0 + a = a\$ l’invariant est donc bien vérifié

  • Dans la boucle :

    • à l’itération \$i\$, on a : \$a = b*quotient_i + reste_i\$

    • à l’itération \$i+1\$, on a : \$a = b*(quotient_i + 1) + (reste_i - b)\$

    • Soit : \$a = b*quotient_i + b + reste_i - b\$

    • Donc : \$a = b*quotient_i + reste_i\$

    • Conclusion : la propriété \$a = b*quotient + reste\$ est toujours vrai dans la boucle

  • A la sortie de la boucle :

    • A la dernière itération on avait \$a = b*quotient_n + reste_n\$ et \$reste_n <= b\$

    • La condition de bouclage n’est plus respectée, on sort de la boucle et la propriété \$a = b*quotient + reste\$ est toujours vrai

  • Conclusion : la propriété \$a = b*quotient + reste\$ est bien l’invariant de boucle. On peut certifier que la fonction donne bien le résultat attendu.

Exercices

Considérons la fonction suivante qui effectue la multiplication de deux nombres entiers a et b avec b>=0 :

def produit(a : int, b : int) -> int:
    ```Retourne produit = a*b avec b>=0```
    if b<0:
        return None
    i = 0
    p = 0
    while i<b:
        p = p + a
        i = i + 1
    return p

Q1) Quelle variable constitue le variant de boucle ?

Q2) Faites tourner l’algorithme de la fonction produit(a,b) à la main et complétez le tableau suivant:

Itération Valeur de i Valeur de p Condition (i < b)

0

0

0

Vrai

1

2

3

…

i

…

i=b

Q3) En déduire l’invariant de boucle.

Considérons maintenant la fonction suivante qui effectue l’élévation à la puissance e d’un nombre n, e et n étant deux nombres entiers avec e>=0 :

def puissance(n : int, e : int) -> int:
    ```Retourne puissance = a^b avec b>=0```
    if e<0:
        return None
    if e==0:
        return 1
    i = 0
    p = 1
    while i<e:
        p = p * n
        i = i + 1
    return p

Q4) Identifiez le variant et l’invariant de boucle en reprenant les questions Q1) à Q3).

Q5) Dans votre environnement de développement, écrivez un programme qui utilisera la fonction produit(), qui demandera à l’utilisateur de fournir les nombre a et b et qui retournera le résultat de la fonction produit(a,b)

Q6) Ecrivez un programme qui utilisera la fonction puissance(), qui demandera à l’utilisateur de fournir les nombre n et e et qui retournera le résultat de la fonction puissance(n,e)

Test

En python l’instruction assert permet de rajouter des contrôles pour le débogage d’un programme. Ils sont un moyen systématique de vérifier que l’état interne d’un programme est conforme aux attentes du développeur, l’objectif étant de détecter les bogues. En particulier, ils sont utiles pour détecter les fausses hypothèses formulées lors de l’écriture du code. En outre, ils peuvent faire office de documentation en ligne en rendant évidentes les hypothèses du développeur.

  • Utilisation basique :

assert a_tester == valeur_attendue

  • Exemple :

a = 3
b = 5
p = a*b
assert p == 15  # le test passe : rien ne s'affiche
assert p == 14  # le test ne passe pas : affichage d'une exception

Q7) Ajoutez dans les fonctions produit() et puissance() trois assertions permettant de vérifiez les invariants de boucle identifiés aux questions Q3) et Q4)

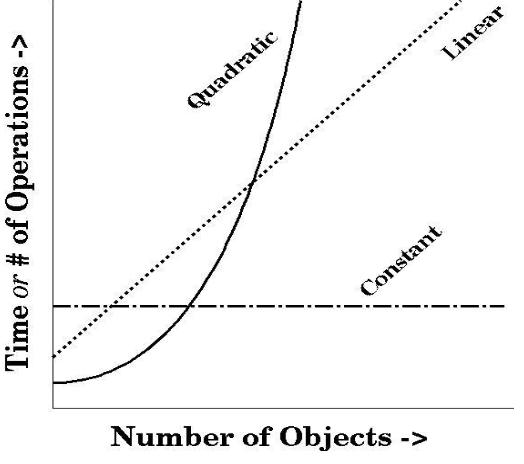
Complexité

Pour identifier la classe de complexité d’un algorithme, il faut s’intéresser à sa durée d’exécution ou plus précisément à comment sa durée d’exécution augmente lorsque la taille des données augmente.

Complexity

Ressource : Berkeley Algorithmic Complexity

Vous allez faire tourner la fonction produit() en jouant tour à tour sur les paramètres a et b pour identifier sa classe de complexité :

Q8) Commencez par faire varier le paramètre b. Ajoutez la fonction suivante à votre programme et faites le tourner.

import time
import matplotlib.pyplot as plt

def complexite(nb_fois_algo : int)->None:
    ```nb_fois_algo : produit(10,n) avec n de 0 à  nb_fois_algo ```
    les_produits = []
    les_times = []
    for n in range(0,nb_fois_algo,10):
        start = time.clock()
        les_produits.append(produit(10,n))
        end = time.clock()
        les_times.append((end-start)*1000)

    plt.plot(les_produits, les_times)
    plt.xlabel('produits de 10*n')
    plt.ylabel('Temps (ms)')
    plt.title("Complexite de l'algorithme de la fonction produit()")
    plt.grid()
    plt.legend()
    plt.show()

def produit(a : int, b : int) -> int:
    ...
if __name__ == '__main__':
    complexite(5000)

Q9) Enregistrez la figure obtenue et identifiez la classe de complexité de l’algorithme.

Q10) Faites varier le paramètre a, faites tourner le programme, enregistrez la figure obtenue et identifier dans ce cas la classe de complexité de l’algorithme.
Expliquez la différence avec le cas précédent.